CS488 Raytracer
Jul 26, 2011

The final scene, demonstrating reflection, refraction, bump mapping, shadows, transparency, and translucency.
Overview
This project was a University project for CS488 – Introduction to Computer Graphics. The primary goal was to explore the implementation of a variety of different textures and materials.
- Hard shadows
- Reflections, various degrees of reflectivity possible
- Glossy surfaces
- Refraction, physically based according to differing indices of refraction
- Texture mapping
- Bump mapping
- 2D/3D procedural textures
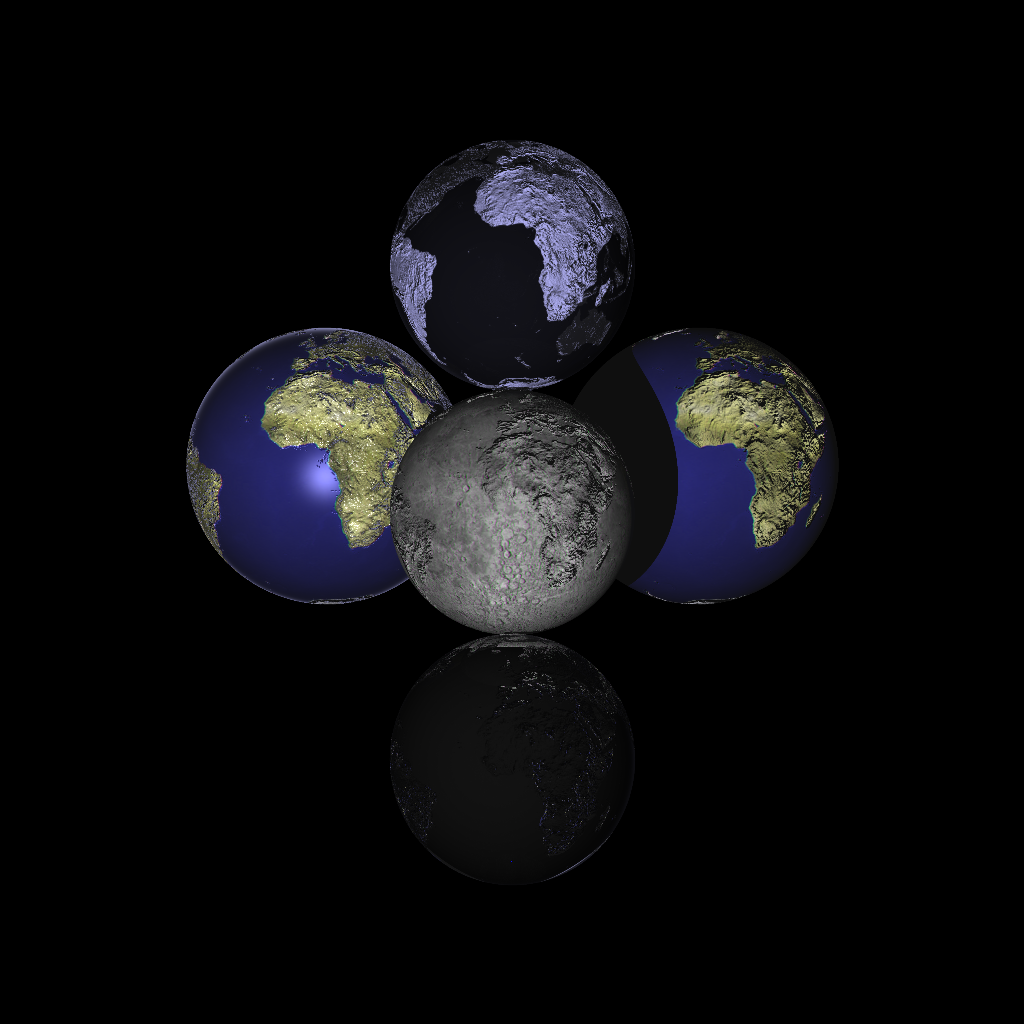
All manners of textured spheres.

Heavy refraction from the front-most glassy sphere.
If you’d like to learn more about the implementation, please consult this (really difficult to consume) documentation.